TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

 TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Em física, o comprimento de onda térmico de Broglie é definido para um gás ideal livre de partículas mássicas em equilíbrio como:

${\displaystyle \Lambda ={\sqrt {\frac {h^{2}}{2\pi mkT}}}={\frac {h}{(2\pi mkT)^{1/2}}}}$

/////////

 TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

• h é a constante de Planck
• m é a massa de um gás de partículas
• k é a constante de Boltzmann
• T é a temperatura do gás

A concentração quântica n_Q é a concentração de partícula (i.e. onúmero de partículas porunidade de volume) de um sistema onde a distância interpartícula é igual ao comprimento de onda térmico de de Broglie ou equivalentemente quando os comprimentos de onda das partículas são tangentes ("se tocam") mas não se sobrepõe.

Efeitos quanticos tornam-se mais apreciáveis quando a concentração de partículas é maior ou igual que a concentração quântica, a qual é definida como:

${\displaystyle n_{Q}=\left({\frac {MkT}{2\pi \hbar ^{2}}}\right)^{3/2}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde:

M é a massa das partículas no sistema

k é a constante de Boltzmann

T é a temperatura medida em kelvin

${\displaystyle \hbar \,}$ é a constante de Planck reduzida

Como a concentração quântica depende da temperatura; altas temperaturas irão colocar a maioria dos sistemas no limite clássico sem estes terem uma densidade muito alta, e.g. como uma anã branca.

O conjunto canónico ^{(português europeu)} ou conjunto canônico ^{(português brasileiro)} ou ensemble canónico ^{(português europeu)} ou ensemble canônico ^{(português brasileiro)} em física estatística é um ensemble estatístico que modeliza um sistema físico em contato com um reservatório térmico de temperatura fixa, supondo que o volume e o número de partículas do sistema também são fixos. O ensemble canônico descreve tipicamente um sistema em contato com um reservatório térmico através de uma parede diatérmica, fixa e impermeável, mas sua aplicação transcende os limites da física.

Para um sistema em equilíbrio assumindo valores discretos de energia, com temperatura, número de partículas e volume fixos por reservatórios, a probabilidade ${\displaystyle p_{i}}$ de encontrá-lo num micro-estado particular ${\displaystyle p_{i}}$ é dada por:

${\displaystyle p_{i}={\tfrac {1}{Z}}e^{-{\frac {E_{i}}{kT}}},}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

sendo ${\displaystyle E_{i}}$ a energia do microestado ${\displaystyle i}$ e ${\displaystyle Z}$ a função de partição do sistema, definida por

${\displaystyle Z=\sum _{i}e^{-{\frac {E_{i}}{kT}}}=\sum _{i}e^{-\beta E_{i}}.}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Fora da física, o formalismo canónico é amplamente utilizado, sendo aplicado, por exemplo, para prever teoricamente a distribuição da rendas da observação de Pareto de que as rendas altas se distribuem de acordo com uma lei potencial inversa. A evidência indica que as rendas altas de diversos lugares dos Estados Unidos se encontram em equilíbrio termodinâmico.

• 5Referências

Apresentação física do problema

Imagine-se que se tem um sistema físico em contacto com um banho térmico. Isto quer dizer que está em contacto com uma grande massa a uma temperatura dada, e pelo princípio zero da termodinâmica tenderemos portanto o sistema em equilíbrio termodinâmico com o banho. Nestas condições, a energia não está totalmente determinada, senão que é uma variável aleatória que pode tomar uma série de valores. Desta forma, só podemos falar de probabilidade de que o sistema adopte uma energia determinada em função desta temperatura.

O fator de Boltzmann

Demonstra-se que a probabilidade de que um sistema a temperatura T esteja numa configuração de energia E é proporcional ao fator de Boltzmann:

${\displaystyle P_{E}={\frac {e^{-E/k_{B}T}}{Z}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde

${\displaystyle P_{E}}$ é a probabilidade buscada

${\displaystyle E}$ é a energia cuja probabilidade se está a procura

${\displaystyle k_{B}}$ é a constante de Boltzmann

${\displaystyle T}$ é a temperatura.

A constante ${\displaystyle Z}$ não é mais que uma constante de normalização imposta para que a soma das probabilidades de todos os estados seja um. Define-se trivialmente como:

${\displaystyle Z=\sum _{\nu }e^{-E_{\nu }/k_{B}T}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde ${\displaystyle \nu }$ é um índice mudo que recorre todos os estados possíveis do sistema com um número de partículas, volume e temperatura dadas.

A função de partição canónica

A constante de normalização ${\displaystyle Z}$ recebe o nome de função de partição canónica ou simplesmente de função partição. Esta é uma função matemática da temperatura, em número de partículas e o volume. Pode-se demonstrar a fórmula seguinte, que relaciona a mecânica estatística com a termodinâmica no conjunto canónico:

${\displaystyle F(T,V,N)=-k_{B}T\;\log {Z}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Esta equação nos dá a energia livre de Helmholtz do sistema (uma variável de estado termodinâmica) em função das suas variáveis naturais, o que supõe um conhecimento termodinâmico exaustivo do sistema. Portanto conhecer a função de partição é resolver o problema estatístico.

A física estatística é o ramo da física que usa métodos da teoria das probabilidades e estatística e, particularmente, as ferramentas matemáticas para lidar com grandes populações e aproximações, na solução de problemas físicos. Pode descrever uma grande variedade de campos com uma natureza inerentemente estocástica. Suas aplicações incluem muitos problemas nos campos da física, biologia, química, neurologia e até mesmo em algumas ciências sociais, como a sociologia. Seu principal objetivo é esclarecer as propriedades da matéria sob conjuntos, em termos de leis físicas que regem o movimento atômico.^[1]

Em particular, a mecânica estatística desenvolve os resultados fenomenológicos da termodinâmica a partir de uma análise probabilística dos sistemas de base microscópica. Historicamente, um dos primeiros tópicos da física onde foram aplicados métodos estatísticos foi o campo da mecânica, que se preocupa com o movimento de partículas ou objetos quando submetidos a uma força.

• 4Leitura adicional

Mecânica estatística

Ver artigo principal: Mecânica estatística

A mecânica estatística fornece um quadro que relaciona as propriedades microscópicas de átomos e moléculas com as propriedades macroscópicas ou extensivas de materiais que podem ser observados na vida cotidiana. Portanto, ela explica a termodinâmica como um resultado natural da estatística, mecânica clássica e mecânica quântica ao nível microscópico. Por causa desta história, a física estatística é muitas vezes considerada como sinônimo de mecânica estatística ou termodinâmica estatística.

Uma das equações mais importantes da mecânica estatística (análogo à F = ma em mecânica, ou a equação de Schrödinger na mecânica quântica) é a definição da função de partição Z, que é essencialmente uma soma ponderada de todos os possíveis estados q disponíveis para um sistema .

${\displaystyle Z=\sum _{q}{\mathrm {e} ^{-{\frac {E(q)}{k_{B}T}}}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde ${\displaystyle k_{B}}$ é a constante de Boltzmann, T é a temperatura e E(q) é a energia do estado q. Além disso, a probabilidade de um determinado estado q ocorrer é dada por

${\displaystyle P(q)={\frac {\mathrm {e} ^{-{\frac {E(q)}{k_{B}T}}}}{Z}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Aqui, vemos que os estados de energia muito alta têm pouca probabilidade de ocorrência, um resultado que é consistente com a intuição.

A abordagem estatística pode funcionar bem em sistemas clássicos quando o número de graus de liberdade (e assim o número de variáveis​​) é tão grande que a solução exata não é possível, ou não é realmente útil. A mecânica estatística também pode descrever o trabalho na dinâmica não-linear, teoria do caos, física térmica, dinâmica dos fluidos (particularmente nos números de Knudsen elevados) e física de plasmas.

Embora alguns problemas em física estatística possam ser resolvidos analiticamente por meio de aproximações e expansões, as pesquisas mais atuais utilizam o poder de processamento de computadores modernos para simular ou aproximar soluções. Uma abordagem comum para problemas estatísticos é usar uma simulação de Monte Carlo para produzir uma ideia da dinâmica de um sistema complexo.

O teorema de Liouville é um resultado da mecânica hamiltoniana sobre a evolução temporal de um sistema mecânico. Considera-se um conjunto de partículas com condições iniciais próximas que podem ser representadas no espaço de fases por uma região conexa, a qual, apesar de se expandir e contrair a medida que cada partícula evolua, manterá invariante seu volume.

Há também resultados matemáticos relacionados em topologia simplética e teoria ergódica.

Consideremos uma região do espaço fásico que evolua com o tempo ao deslocar-se sobre sua trajetória. Cada um de seus pontos transforma-se ao longo do tempo em uma região de localizada forma diferente, a qual se situa em outra parte do espaço fásico. O teorema de Liouville afirma que, apesar da translação e a alteração de forma, o "volume" total desta região permanecerá invariante. Além disso, devido à continuidade da evolução temporal, se a região for conexa inicialmente, seguirá sendo conexa todo o tempo.

Quase todas as demostrações usam o fato de que a evolução temporal de uma "nuvem" de pontos no espaço fásico é de fato uma transformação canônica que alterará a forma e posição de tal nuvem, ainda que mantenha seu volume total.

• 5Referências

Demonstração direta

Uma forma de ver provada que a evolução temporal é uma transformação canônica, fato relativamente perceptível, e a partir daí calcular diretamente o determinante de tal alteração de coordenadas, é provar que de fato o determinante de tal transformação é igual a 1, o qual prova a invariância do volume.

Demonstração baseada na forma simplética

Outra forma de provar o teorema é ter em conta que a forma de volume ${\displaystyle {\eta }_{\Gamma }\;}$ do espaço fásico é o n-ésimo produto da forma simplética, e que está de acordo com o teorema de Darboux, expressando-se como produto de pares de variáveis canonicamente conjugadas:

${\displaystyle {\eta }_{\Gamma }=\bigwedge _{i=1}^{n}\omega =\omega \land \dots \land \omega =dp_{1}\land \dots \land dp_{n}\land dq_{1}\land \dots \land dq_{n}=dP_{1}\land \dots \land dP_{n}\land dQ_{1}\land \dots \land dQ_{n}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

De onde segue que o determinante da transformação é igual a 1 e, portanto:

${\displaystyle \forall V\subset \Gamma :\quad \int _{V}d^{n}\mathbf {q} d^{n}\mathbf {p} =\int _{\phi _{\tau }(V)}d^{n}\mathbf {Q} d^{n}\mathbf {P} }$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Essa última expressão é essencialmente o enunciado do teorema de Liouville.

Equação de Liouville

O teorema de Liouville pode ser reescrito em termos do colchete de Poisson. Essa forma alternativa, conhecida como equação de Liouville, vem a ser dada por:

${\displaystyle {\frac {\partial \rho }{\partial t}}=-\{\,\rho ,H\,\}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ou em termos do operador de Liouville, também chamado "Liouvilliano":

${\displaystyle {\hat {\mathbf {L} }}=\sum _{i=1}^{d}\left[{\frac {\partial H}{\partial p_{i}}}{\frac {\partial }{\partial q^{i}}}-{\frac {\partial H}{\partial q^{i}}}{\frac {\partial }{\partial p_{i}}}\right],}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

que leva à forma:

${\displaystyle {\frac {\partial \rho }{\partial t}}+{\hat {\mathbf {L} }}\rho =0.}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Mecânica quântica

Em mecânica quântica existe um resultado análogo ao teorema de Liouville que descreve a evolução de um estado misto. De fato, pode-se chegar à versão mecânico-quântica deste resultado mediante a simples quantização canônica. Aplicando esse procedimento formal, chegamos ao análogo quântico do teorema de Liouville:

${\displaystyle {\frac {\partial }{\partial t}}\rho =-{\frac {i}{\hbar }}[H,\rho ]}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Onde ρ é a matriz densidade. Quando se aplica o resultado ao valor esperado de um observável, a correspondente equação dada pelo teorema de Ehrenfest toma a forma:

${\displaystyle {\frac {d}{dt}}\langle A\rangle ={\frac {i}{\hbar }}\langle [H,A]\rangle }$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Onde ${\displaystyle A\,}$ é um observável.

Em Mecânica estatística, um ensemble microcanônico é o conjunto estatístico que é usado para representar os possíveis estados de um sistema mecânico que tem uma energia total especificada. O sistema é assumido como isolado, no sentido que o sistema não pode trocar energia ou partículas com seu ambiente, assim o valor da energia total permanece fixo enquanto o tempo passa. A energia, volume, e composição do sistema são mantidas fixas em todos os estados possíveis do sistema.

As variáveis ​​macroscópicas do conjunto microcanônico são parâmetros físicos que influenciam a natureza dos estados internos do sistema, como o número total de partículas ${\displaystyle N}$, o volume disponível ${\displaystyle V}$, bem como a energia total ${\displaystyle E}$. Em consequência, este conjunto é algumas vezes chamado de ensemble ${\displaystyle NVE}$, pois cada um destes três parâmetros é uma constante no conjunto.

Em termos simples, o ensemble microcanônico é definido através da atribuição de uma probabilidade igual para cada microestado do sistema cuja energia cai dentro de um intervalo ${\displaystyle E}$ e ${\displaystyle E+\Delta E}$. Para todos os outros microestados se assume probabilidade igual a zero. Seja ${\displaystyle P_{i}(E)}$ a probabilidade de o sistema estar em um dado microestado ${\displaystyle i}$ naquele intervalo de energia. O sistema deve estar em um dado microestado, logo

${\displaystyle \sum _{i}P_{i}(E)=1}$ .

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Se o número total de microestados com igual probabilidade é ${\displaystyle W(E)}$, então

${\displaystyle P_{i}(E)={\frac {1}{W(E)}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

O intervalo de energia é, em seguida, reduzido em largura até que se torne infinitamente estreito, ${\displaystyle \Delta E\rightarrow 0}$. No limite deste processo, obtém-se o conjunto microcanônico.

Na prática, o ensemble microcanônico não corresponde a uma situação experimentalmente realista. Para um sistema físico real, existe alguma incerteza na energia devido a fatores não controlados na preparação do sistema. Além da dificuldade de encontrar um análogo experimental, é difícil de realizar cálculos que satisfaçam exatamente o requisito de energia fixa. Sistemas em equilíbrio térmico com o ambiente têm incerteza na energia, e são melhor descritos usando o ensemble canônico ou o ensemble grande canônico.

Espaço de fases de um sistema dinâmico com estabilidade focal.

Espaço de fases ou espaço fásico é definido como o espaço formado pelas posições generalizadas e seus momentos conjugados correspondentes. Se emprega no contexto da mecânica lagrangiana e a mecânica hamiltoniana. Usualmente se designa o espaço fásico ou uma parte dele por Γ (gamma maiúscula). Fisicamente cada ponto do espaço fásico representa um possível estado do sistema mecânico.

Em física estatística se usam distribuições de probabilidade definidas sobre o espaço fásico. Partindo de certo subconjunto das distribuições de probabilidade de um espaço fásico pode construir-se uma estrutura de espaço de Hilbert. Estes espaços de Hilbert de um sistema clássico são a base para os espaços de Hilbert que aparecem na mecânica quântica.

• 5Ligações externas

Espaço de fases na mecânica clássica

Em mecânica clássica o espaço de fases é uma construção matemática a partir do espaço de configuração. Concretamente um espaço de fases adequado para um sistema com um número finito de graus de libertade é um fibrado tangente do espaço de configuração do sistema mecânico. Esse fibrado tangente construído dessa maneira pode ainda ser dotado de uma topologia simplética onde podem formular-se convenientemente os teoremas da mecânica hamiltoniana.

Um dos teoremas clássicos sobre espaços de fases é o teorema de Liouville, segundo o qual uma nuvem de pontos distribuídos de acordo com uma densidade de probabilidade que represente um estado de equilíbrio macroscópico ρ(p_i,q_i) deve ser invariável no tempo.

Além disto cada hamiltoniano H definido sobre um espaço de fases está associado a um conjunto de trajetórias de evolução temporal. O conjunto de trajetórias constitui uma foliação unidimensional do espaço de fases que recobre quase todo o espaço de fases (concretamente todo o espaço de fases, salvo um conjunto de medida nula), este último equivale a que o espaço pode ser descomposto em trajetórias que não se intersectam.

Espaço de fases em mecânica quântica

Uma das características distintas da mecânica quântica é que o estado físico de um sistema não determina o resultado de qualquer medida que possa fazer-se sobre ele. Em termos mais simples, o resultado de uma medida sobre dois sistemas quânticos que tenham o mesmo estado físico nem sempre resulta nos mesmos resultados. Assim uma teoria como a mecânica quântica que trata de descrever a evolução temporal dos sistemas físicos só pode prever a probabilidade de que ao medir uma determinada grandeza física se obtenha determinado valor. Isto quer dizer que a mecânica quântica realmente é uma teoria que explica como varia a distribuição de probabilidade das possíveis medidas de um sistema (entre duas medições consecutivas, já que no instante da medida se produz um colapso da função de onda aleatório).

O estado quântico de um sistema pelas razões anteriormente expostas não se parece em nada ao estado clássico de uma partícula ou um sistema de partículas. De fato o estado quântico de um sistema é representável mediante uma função de onda:

$${\displaystyle \Phi \in L_{\mu }^{2}(\Gamma )}$$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

A relação mais próxima entre espaço fásico e função de onda é que o quadrado do módulo da função de onda está relacionado com uma distribuição de probabilidade definida sobre o espaço fásico. Isto significa que, para construir o conjunto de estados quânticos ou espaço de Hilbert de certos sistemas quânticos, pode considerar-se inicialmente o espaço fásico que se usaria em sua descrição clássica e considerar o conjunto de funções de quadrado integrável sobre o espaço fásico, a este tipo de procedimento se conhece como quantização.

Quantização a partir do espaço fásico clássico

Ver artigo principal: Quantização

Em física estatística se empregam distribuições de probabilidade sobre o espaço fásico, este conjunto de distribuições de probabilidade pode dotar-se de estrutura de espaço de Hilbert. É precisamente sobre esta abstração última que se constrói a mecânica quântica onde não se empregam espaços de configuração, senão diretamente espaços de Hilbert. O estado de um sistema quântico se define como uma "função de onda" que não é outra coisa que um elemento ou vetor deste espaço de Hilbert (concretamente o estado do sistema é uma classe de equivalência de vetores do espaço de Hilbert).

A constante de Boltzmann (${\displaystyle k}$ ou ${\displaystyle k_{B}}$) é a constante física que relaciona temperatura e energia de moléculas.^[1] Tem o nome do físico austríaco Ludwig Boltzmann, que fez importantes contribuições para a física e para a mecânica estatística, na qual a sua constante tem um papel fundamental. A 26ª Conferência Geral de Pesos e Medidas fixou o valor exato da constante de Boltzmann:^[2]

${\displaystyle k=1,380\ 649\times 10^{-23}\ {\mbox{J}}\cdot {\mbox{K}}^{-1}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

• 6Ligações externas

História

Embora Boltzmann tenha feito primeiro a ligação entre entropia e probabilidade, em 1877, a relação não foi expressa com uma constante antes de Max Planck fazê-lo. ${\displaystyle k}$, com um valor preciso de 1.346×10⁻²³ ${\displaystyle {\frac {J}{K}}}$ (apenas 2,5% menor que o conhecido hoje), introduzido na lei de Planck para a radiação do corpo negro, em 1900-1901, no mesmo artigo em que Planck introduziu a constante que leva seu nome, a relação entre a frequência e energia de fótons e a equação de Boltzmann-Planck (por vezes chamada apenas de equação de Boltzmann).^[3]

Determinação experimental

A forma mais simples de chegar à constante de Boltzmann é dividir a constante dos gases perfeitos pela constante de Avogadro.

A constante de Boltzmann relaciona assim a ideia de que, para qualquer quantidade de um gás ideal, obtemos um valor constante caso dividirmos o valor obtido a partir da multiplicação de pressão e volume pelo valor da temperatura, o ${\displaystyle R}$ ${\displaystyle {\bigg (}0,082{\frac {({atm}\cdot L)}{({mol}\cdot K)}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

 ou ${\displaystyle 8,31{\frac {J}{{mol}\cdot K}}{\bigg )}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

. Deste modo estamos a considerar que ${\displaystyle R}$ é a quantidade de energia por mol de moléculas de gás. Ao dividir este novo valor pelo número de Avogadro obtemos a quantidade de energia contida por cada molécula de gás, de acordo com as expressões:

${\displaystyle {\frac {PV}{T}}={cte}(R\cdot n)}$,

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

${\displaystyle {\frac {R}{N}}=K_{b}}$ (ou ${\displaystyle B}$)

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Valores da constantes de Boltzmann em unidades diferentes

Valores de ${\displaystyle k_{B}}$	Unidades	Comentários
${\displaystyle 1.380\ 649\times 10^{-23}}$	J/K	Unidades do SI, valor de 2017 do CODATA, ${\displaystyle {\frac {\mbox{J}}{\mbox{K}}}={\frac {{\mbox{m}}^{2}\cdot {\mbox{kg}}}{({\mbox{s}}{^{2}}\cdot {\mbox{K}})}}}$ na unidades do SI [1]
${\displaystyle {\mbox{8.617 3324 (78)}}\cdot ~10^{-5}}$	eV/K	Valores do CODATA [1] 1 electronvolt ${\displaystyle ={\mbox{1.602 176 565 (35)}}\cdot ~10^{-19}~J}$[1]${\displaystyle {\frac {1}{k_{B}}}={\mbox{11 604.519 (11)}}~{\frac {K}{eV}}}$
${\displaystyle {\mbox{2.083 6618 (19)}}\cdot 10^{10}}$	Hz/K	Valores do CODATA[1] ${\displaystyle 1Hz\cdot }$ h ${\displaystyle ={\mbox{6.626 069 57 (29)}}\cdot 10^{-34}J}$[1]
${\displaystyle {\mbox{3.166 8114 (29)}}\cdot 10^{-6}}$	EH/K	${\displaystyle E_{H}=2}$R∞${\displaystyle hc={\mbox{4.359 744 34 (19)}}\cdot 10^{-18}J}$[1] ${\displaystyle ={\mbox{6.579 683 920 729 (33)}}~Hz\cdot h}$[1]
${\displaystyle {\mbox{1.380 6488 (13)}}\cdot 10^{-16}}$	erg/K	Sistema CGS, 1 erg = ${\displaystyle 1\cdot 10^{-7}J}$
${\displaystyle {\mbox{3.297 6230 (30)}}\cdot 10^{-24}}$	cal/K	1 Caloria ${\displaystyle =4.1868J}$
${\displaystyle {\mbox{1.832 0128 (17)}}\cdot 10^{-24}}$	cal/°R	1 grau de Rankine ${\displaystyle ={\frac {5}{9}}K}$
${\displaystyle {\mbox{5.657 3016 (51)}}\cdot 10^{-24}}$	ft lb/°R	1 força de pés - libras ${\displaystyle ={\mbox{1.355 817 948 331 4004}}~J}$
${\displaystyle {\mbox{0.695 034 76 (63)}}}$	cm−1/K	Valor do CODATA[1] ${\displaystyle 1cm^{-1}{hc}={\mbox{1.986 445 683 (87)}}\cdot 10^{-23}~J}$
${\displaystyle {\mbox{0.001 987 2041 (18)}}}$	kcal/(mol·K)	na forma molar, frequentemente usado em mecânica estatística, usa-se caloria termoquímica = 4.184 Joule
${\displaystyle {\mbox{0.008 314 4621 (75)}}}$	kJ/(mol·K)	na forma molar frequentemente usado em mecânica estatística.
${\displaystyle 4.10}$	${\displaystyle pN\cdot nm}$	${\displaystyle k_{B}}$ em nanômetros por piconewton em 24°C, usado na Biofísica.
${\displaystyle {\mbox{-228.599 1678 (40)}}}$	dBW/K/Hz	em decibel watts, usado nas telecomunicações (Veja Ruído de Johnson–Nyquist)
${\displaystyle {\mbox{1.442 695 041}}\cdot \cdot \cdot }$	bit	em bits (logaritmo com base 2), usado na Entropia da informação ${\displaystyle {\bigg (}}$valor exato é ${\displaystyle {\frac {1}{\ln 2}}{\bigg )}}$
${\displaystyle 1}$	nat	em nats (logaritmo com base ${\displaystyle e}$), usado na Entropia da informação (veja Unidades de Planck)

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Ver também

Em física a Distribuição de Boltzmann permite calcular a função distribuição para um número fracionário de partículas N_i / N ocupando um conjunto de estados i cada um dos quais tem energia E_i:

${\displaystyle {{N_{i}} \over {N}}={{g_{i}e^{-E_{i}/k_{B}T}} \over {Z(T)}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde ${\displaystyle k_{B}}$ é a constante de Boltzmann, T é a temperatura (admitida como sendo uma quantidade precisamente bem definida), ${\displaystyle g_{i}}$ é a degeneração, ou número de estados tendo energia ${\displaystyle E_{i}}$, N é o total do número de partículas:

${\displaystyle N=\sum _{i}N_{i}\,}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

e Z(T) é chamada função partição, a qual pode ser tratada como sendo igual a

${\displaystyle Z(T)=\sum _{i}g_{i}e^{-E_{i}/k_{B}T}.}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Alternativamente, para um sistema único em uma temperatura bem definida, ela dá a probabilidade deste sistema em seu estado específico. A distribuição de Boltzmann aplica-se somente à partículas em uma suficiente alta temperatura e baixa densidade nas quais efeitos quânticos possam ser ignorados, e cujas partículas obedeçam a estatística de Maxwell–Boltzmann. (Veja este artigo para uma derivação da distribuição de Boltzmann.)

A distribuição de Boltzmann é frequentemente expressa em termos de β = 1/kT aonde β refere-se ao beta termodinâmico. O termo ${\displaystyle e^{-\beta E_{i}}}$ ou ${\displaystyle e^{-E_{i}/(kT)}}$, o qual dá a relativa probabilidade (não normalizada) de um estado, é chamada factor de Boltzmann e aparece frequentemente no estudo da física e química.

Quando a energia é simplesmente a energia cinética da partícula

${\displaystyle E_{i}={\begin{matrix}{\frac {1}{2}}\end{matrix}}mv^{2},}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

então a distribuição corretamente dá a distribuição de Maxwell-Boltzmann das velocidades das moléculas do gás, previamente previstas por Maxwell em 1859. A distribuição de Boltzmann é, entretanto, muito mais geral. Por exemplo, ela prediz a variação da densidade de partículas num campo gravitacional em relação à altitude, se ${\displaystyle E_{i}={\begin{matrix}{\frac {1}{2}}\end{matrix}}mv^{2}+mgh}$. De fato a distribuição aplica-se sempre que as considerações quânticas possam ser ignoradas.

Em alguns casos, uma aproximação contínua pode ser usada. Se há g(E) dE estados com energia E a E + dE, quando a distribuição de Boltzmann prediz uma probabilidade de distribuição para a energia:

${\displaystyle p(E)\,dE={g(E)\exp({-\beta E}) \over {\int g(E')\exp {(-\beta E')}}\,dE'}\,dE.}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Quando g(E) é chamado densidade de estado se o espectro de energia é contínuo.

Partículas clássicas com esta distribuição de energia são ditas obedientes à estatística de Maxwell–Boltzmann.

No limite clássico, i.e. em grandes volumes de E/kT ou às menores densidades de estados — quando funções de onda de partículas praticamente não se sobrepõe, tanto a distribuição Bose–Einstein ou a Fermi–Dirac tornam-se a distribuição de Boltzmann.

Em mecânica estatística, a estatística Maxwell–Boltzmann descreve a distribuição estatística de partículas materiais em vários estados de energia em equilíbrio térmico, quando a temperatura é alta o suficiente e a densidade é baixa suficiente para tornar os efeitos quânticos negligenciáveis. A estatística Maxwell–Boltzmann é consequentemente aplicável a quase qualquer fenômeno terrestre para os quais a temperatura está acima de poucas dezenas de kelvins.^[1][2]

O número esperado de partículas com energia ${\displaystyle \epsilon _{i}}$ para a estatística de Maxwell–Boltzmann é ${\displaystyle N_{i}}$ onde:

${\displaystyle {\frac {N_{i}}{N}}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}}}={\frac {g_{i}e^{-\epsilon _{i}/kT}}{Z}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde:

• ${\displaystyle N_{i}}$ é o número de partículas no estado i
• ${\displaystyle \epsilon _{i}}$ é a energia do estado i-ésimo
• ${\displaystyle g_{i}}$ é a degenerescência do nível de energia i, o número de estados dos partículas (excluindo o estado de "partícula livre") com energia ${\displaystyle \epsilon _{i}}$
• ${\displaystyle \mu }$ é o potencial químico
• ${\displaystyle k}$ é a constante de Boltzmann
• ${\displaystyle T}$ é a temperatura absoluta
• ${\displaystyle N}$ é o número total de partículas

${\displaystyle N=\sum _{i}N_{i}\,}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

• ${\displaystyle Z}$ é a função partição

${\displaystyle Z=\sum _{i}g_{i}e^{-\epsilon _{i}/kT}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

• ${\displaystyle e^{(...)}}$ é a função exponencial, sendo e o número de Euler

A distribuição de Maxwell-Boltzmann tem sido aplicada especialmente à teoria cinética dos gases, e outros sistemas físicos, além de em econofísica para predizer a distribuição da renda. Na realidade a distribuição de Maxwell-Boltzmann é aplicável a qualquer sistema formado por N "partículas" ou "indivíduos" que interacambiam estacionariamente entre si uma certa magnitude ${\displaystyle m}$ e cada um deles têm uma quantidade ${\displaystyle m_{i}}$ da magnitude ${\displaystyle m}$ e ao longo do tempo ocorre que ${\displaystyle \sum _{i=1}^{N}M=m_{1}+m_{2}+...+m_{N}}$.

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Limites de aplicação

Para um sistema de partículas quânticas, a hipótese de que ${\displaystyle N_{i}}$ seja substancialmente menor que ${\displaystyle g_{i}}$ para os estados diferentes do fundamental em geral não se cumprirá e é necessário recorrer-se à estatística de Bose-Einstein se as partículas são bosônicas ou à estatística de Fermi-Dirac se as partículas são fermiônicas.

As estatísticas de Bose–Einstein e Fermi–Dirac podem ser expressas como:

${\displaystyle N_{i}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}\pm 1}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Assumindo que o valor mínimo de ${\displaystyle \epsilon _{i}}$ é bastante pequeno, se pode verificar que a condição na qual a distribuição de Maxwell-Boltzmann é válida é quando se cumpre que:

${\displaystyle e^{-\mu /kT}\gg 1}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Para um gás ideal, podemos calcular os potenciais químicos utilizando o desenvolvimento da equação de Sackur–Tetrode para demonstrar que:

${\displaystyle \mu =\left({\frac {\partial E}{\partial N}}\right)_{S,V}=-kT\ln \left({\frac {V}{N\Lambda ^{3}}}\right)}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

onde ${\displaystyle E}$ é a energia interna total, ${\displaystyle S}$ é a entropia, ${\displaystyle V}$ é o volume, e ${\displaystyle \Lambda }$ é o comprimento de onda térmico de de Broglie. A condição de aplicação para a distribuição Maxwell-Boltzmann em um gás ideal resulta:

${\displaystyle {\frac {V}{N\Lambda ^{3}}}\gg 1.}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Distribuição de Fermi-Dirac em função de ε/μ para quatro temperaturas diferentes.

Em mecânica estatística, a estatística de Fermi-Dirac é uma estatística quântica que descreve o comportamento de sistemas de partículas com spin semi-inteiro, os férmions. Leva o nome de dois eminentes físicos: Enrico Fermi e Paul Adrien Maurice Dirac cada um dos quais descobriu o método de forma independente (embora Fermi tenha definido as estatísticas antes de Dirac).^[1][2] Antes do estudo da estatística de Fermi-Dirac é necessário compreender algumas diferenças entre sistemas clássicos e quânticos. Sistemas clássicos são formados, a priori, por partículas distinguíveis, ou seja, é possível identificar e diferenciar tais partículas individualmente e nestes sistemas os efeitos quânticos são desprezíveis, sendo o sistema descrito pela estatística de Maxwell–Boltzmann. Já sistemas quânticos são formados por partículas indistinguíveis, devido à superposição de suas funções de onda, ou seja é impossível descrevê-las individualmente e neste sistema os efeitos quânticos devem ser considerados. Sistemas quânticos podem ser descritos pelas estatística de Fermi-Dirac ou de Bose-Einstein, dependendo do spin das partículas.^[3][4]

• 5Referências

Formulação matemática

Como as partículas são indistinguíveis na estatística de Fermi-Dirac, a especificação do número de partículas é suficiente para determinarmos o estado do gás. Como os férmions obedecem ao princípio de exclusão de Pauli, não é possível que mais que uma partícula esteja no mesmo estado, se faz apenas necessário somar sobre todos os números possíveis de partículas em um único estado, ou seja, os dois possíveis valores ^[5]:

${\displaystyle n_{r}=0,1}$ para cada ${\displaystyle r}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Quando o número total de partículas ${\displaystyle N}$ é fixado, a soma sobre todos os valores possíveis de ${\displaystyle n_{r}}$, com ${\displaystyle n_{1},n_{2},...}$ segue a seguinte relação

${\displaystyle \sum _{r}n_{r}=N}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

Dado um sistema com ${\displaystyle N}$ férmions em equilíbrio térmico a uma temperatura arbitrária ${\displaystyle T}$, o número médio de partículas ${\displaystyle <n_{s}>}$ em um estado particular ${\displaystyle s}$ com energia ${\displaystyle \epsilon _{s}}$ é obtido através da distribuição canônica, logo^[5]

${\displaystyle <n_{s}>={\frac {\sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}{\sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}}}$

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

no qual ${\displaystyle \beta ={\frac {1}{k_{B}T}}}$, 

${\displaystyle Z_{s}(N)=\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}$

Somando sobre ${\displaystyle n_{s}}$ = 0 e 1, temos

${\displaystyle <n_{s}>={\frac {e^{-\beta \epsilon _{s}}Z_{s}(N-1)}{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)}}}$

ou, ainda, podemos simplificar:

${\displaystyle <n_{s}>={\frac {1}{[Z_{s}(N)/Z_{s}(N-1)]e^{\beta \epsilon _{s}}+1}}}$

Na condição em que ${\displaystyle \Delta N\ll N}$, podemos escrever

${\displaystyle lnZ_{s}(N-\Delta N)=lnZ_{s}(N)-{\frac {\partial lnZ_{s}}{\partial N}}\Delta N=lnZ_{s}(N)-\alpha _{s}\Delta N}$

${\displaystyle Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}}$

com ${\displaystyle \alpha _{s}={\frac {\partial lnZ_{s}}{\partial N}}}$. Como ${\displaystyle Z_{s}(N)}$ é uma soma sobre muitos estados, a variação de seu logaritmo com o número de partículas total ${\displaystyle N}$ não é afetado por qual estado particular ${\displaystyle s}$ foi omitido no somatório. Portanto, podemos fazer uma aproximação em que ${\displaystyle \alpha _{s}}$ é independente de ${\displaystyle s}$:

${\displaystyle \alpha _{s}=\alpha }$

Ainda, podemos aproximar ${\displaystyle \alpha }$ em termos da derivada da função partição ${\displaystyle \mathrm {Z} (N)}$ sobre todos os estados, assim^[5]:

${\displaystyle \alpha ={\frac {\partial ln\mathrm {Z} }{\partial N}}}$

Se utilizarmos ${\displaystyle \Delta N=1}$ na aproximação, encontraremos a distribuição de Fermi-Dirac^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\alpha +\beta \epsilon _{s}}+1}}}$

Ainda, o parâmetro ${\displaystyle \alpha }$ pode ser determinado pela primeira condição feita nesta dedução, em que

${\displaystyle \sum _{r}<n_{r}>=N}$

ou

${\displaystyle \sum _{r}{\frac {1}{e^{\alpha +\beta \epsilon _{r}}+1}}=N}$

Da relação entre a função partição ${\displaystyle Z}$ e a energia livre de Helmholtz ${\displaystyle F}$, sabemos que ${\displaystyle F=-k_{B}Tln\mathrm {Z} }$, logo:

${\displaystyle \alpha =-{\frac {1}{k_{B}T}}{\frac {\partial F}{\partial N}}=-{\frac {\mu }{kT}}}$

${\displaystyle \alpha =-\beta \mu }$

onde ${\displaystyle \mu }$ é o potencial químico. Então outra forma de se definir a distribuição de Fermi-Dirac é^[5]:

${\displaystyle <n_{s}>={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}+1}}}$

Quando os níveis de energia são muito próximos, de modo que podemos considerar que formam um contínuo, o número médio de partículas com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$, pode ser escrito como^[5]

${\displaystyle n(\epsilon )=g(\epsilon )F(\epsilon )d\epsilon }$

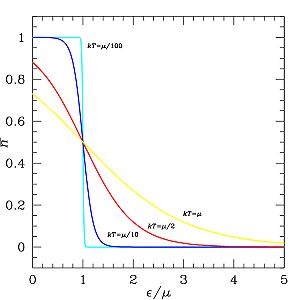
Onde ${\displaystyle g(\epsilon )}$ é a densidade de estados, de modo que ${\displaystyle g(\epsilon )d\epsilon }$ fornece o número de estados com energia entre ${\displaystyle \epsilon }$ e ${\displaystyle \epsilon +d\epsilon }$. E ${\displaystyle F(\epsilon )}$ é a chama função de Fermi, dada por^[5]

${\displaystyle F(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}}$

Interpretação física

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

sendo ${\displaystyle k_{B}}$ a constante de Boltzmann. Podemos renomear alguns termos na expressão acima, de forma que obtemos

Na mecânica estatística, a fórmula de entropia de Boltzmann (também conhecida como equação de Boltzmann-Planck), é uma equação que permite calcular a entropia e o número de micro-estados de um sistema específico.^[2] A fórmula de Boltzmann mostra a relação entre a entropia e o número de maneiras pelas quais os átomos ou moléculas de um sistema termodinâmico podem ser organizadas.^[3]

Definição

A fórmula de Boltzmann é uma equação de probabilidade que relaciona a entropia S de um gás ideal com a quantidade W, o número de micro-estados reais correspondentes ao macro-estado do gás:

${\displaystyle S=k_{\mathrm {B} }\ln W}$

///////// TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL.  TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

(1)

onde k_B é a constante de Boltzmann (também escrita como k), que é igual a 1.380649 × 10⁻²³ J/K.^[4][5]

Esta fórmula está gravada no túmulo de Boltzmann (em Viena) na forma:

/////////

TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

${\displaystyle S=k\,log\,W}$

(2)